A sideways look at economics

When he was a young man, my father-in-law, Anthony (Tony) Morgan, CMG, ret. (more usually known as ‘Mogs’), once remarked to his mother-in-law that he found the peas on his plate to be unusually tasty.

It was just a courtesy, really. He could equally well have remained silent or have made a remark about the weather. It was lightly done.

The meal had been proceeding as they usually did. Perhaps he felt it was his turn to say something. Perhaps there had been a period of silence that was too long and had become strained. We all know the feeling of anxiety that grows, sometimes, when silences go on for too long. Pregnant silences. But who could have guessed what a momentous birth would issue from that silence!

At the moment he spoke, just for a blink, time froze, the birds stopped singing, the earth stopped spinning, the planets halted in their courses. The matrix glitched. He had made an intervention, a caesura that, thanks to its timing, somehow changed everything.

The wave function collapsed, and a new one formed, changed.

It turned out that those peas had come from a tin. Tony liked them. The family nostrum, handed down through the subsequent generations, uttered with sage nods and universal assent: “Tony likes tins”, was born.[1]

Thereafter, at any family meal throughout the extended family, it was remembered that the chef must make a special effort to use tinned food whenever Tony was present. People who would normally prefer fresh ingredients would go out of their way to design recipes that involved tinned food, for it was written: Tony likes tins.

Of course, it didn’t matter how much he protested to the contrary that he had no strong feelings about tins either way. That was just him being polite. Everyone knew their duty, there can have been no mistake. They would chuckle as he said things like: “No, I insist, make whatever you would normally make!” They would nod, indulging him, noting inwardly his noble instinct towards self-sacrifice. And they would use tins anyway.

By declaring a preference (then parsed via a step of incorrect deductive logic), the pattern of his life was changed once and for all. He made an observation at a particular time and the folk memory of that changed the pattern of all future choices that would be available to him.

We make choices like that in matters great and small, on a daily basis (though we don’t often realise how important they are), driven by a sense of tension or anxiety, or sometimes just by accident. We interrupt the flow.

For example, when Fathom makes a pitch to a potential prospect. We will typically have spent some time – months, on some occasions – thinking hard about who this prospect is, what their needs might be, how we can fit those needs, and so on. We will have contacted them once, twice or many times. And then the pitch: we roll the dice. We pick up the cup that contains the dice, we shake it, we toss the dice into the air, and then we wait.

The waiting is painful. It induces anxiety and stress. We start to feel that we’d rather just know, even if the answer is ‘no’. We start to think: I wonder what the dice would say if I looked at them now? The temptation is to reach out to the prospect, to ask them to reveal something about how they are thinking: how are the dice likely to fall?

Sometimes, we do just that, interrupting the flow.

Mostly they won’t tell us until they are ready, or at best they will give hints. Whatever the response, we then spend time reading between the lines to get some kind of idea, if we can, from very limited information. We conclude things like it’s a 40% shot: extremely low-information conclusions like that, but at least the anxiety is partially relieved.

Sometimes, though, they respond with a firm answer – probably sooner than they had originally intended.

Either way, if the eventual answer is ‘no’, we then reflect that perhaps we should not have hurried them – maybe by doing that we irritated them enough to change the outcome against us. Maybe it would have been ‘yes’ if we’d just left them alone to decide in their own time.

Equally, if the eventual answer is ‘yes’, we reflect on how wise we were to hurry the process along a bit.

It’s a bit like dating (though I’m happy to report that it’s more than 39 years since I’ve had to worry about that). Suppose you catch someone’s eye across a bar: should you approach that person? Or should you just let things evolve as they will? After a first date, should you call immediately or leave it a few days? You want to know what they are thinking, but if you ask them, will that change what they are thinking?

Can the attempt to observe a process before it is complete change the outcome once it is complete?

In economics, we generally assume that observation is neutral, having no impact on the likelihood of different outcomes. If I know the disposition and momentum of the variables I am trying to model at a given time, then that’s all I need to project their future paths probabilistically to any future time; and I can observe that disposition and momentum whenever I like without changing that structure.[2]

Observing a variable in economics means measuring it. Different variables are measured at different frequencies (annual, quarterly, monthly, daily, intra-day in the case of some financial market data). That frequency is the delta in time between different measurements of the same concept: the ‘dt’. In most cases, dt can be as large or as small as the data permit. You can slice up time into many or few subdivisions, without effect.

The interval between observations is usually assumed to be infinitely divisible, without changing the ex-post trajectory of the variable being observed or the ex-ante probability distribution capturing its possible future trajectories. That is how we normally think about economic variables. I can think of a change of +12 over the year as arising in one step or in four or twelve or n steps: the change of +12 over the year is the same, ex post, in all cases. It was always going to be +12, no matter how many steps I sliced it into.

However, as the example of a pitch or a date illustrates, that’s not usually how we think about uncertainty in our lived experience. It is natural to be concerned that our observation changes the probability distribution of possible trajectories of the variable being observed. This idea is captured in the concept of ‘indivisible stochastic processes’. The dice are in the air: you can’t observe their disposition now without changing their trajectory. In the extreme case, you can’t know how they would fall if they were to fall now, without forcing them to fall now (eg by slamming them down onto the table with your hand). That kind of observation clearly changes their trajectory: where they wind up at (t+1) is now highly likely to be different than it would have been had you let them fall naturally rather than arresting their natural trajectory at (t+0.25). You’ve divided an indivisible process: now it has become something else.

Think about this in terms of some real-world economic variable, let’s say inflation. Suppose we only observed inflation once a year, say in early January, and it covered the whole of the calendar year just gone.

Now imagine that, in February, there is a big shock to oil prices, which increase by $20 per barrel, with proportionate impacts on the cost of energy. Then, in September, oil prices go down again back to where they started. By the time general price inflation is next measured, the following January, the outcome is a draw from a probability distribution whose mean is the inflation target (for example). The path of oil prices along the way has made no difference.

Suppose, now, that we measured prices every month. In that case, after the February oil price shock, we would observe higher prices for a time, and then, after September, prices would fall back again. Once again, by January of the following year, general price inflation would settle at a draw from a probability distribution whose mean was the inflation target – exactly as before.

So, in this case, dividing up the year into twelve dts makes no difference to general price inflation, even though energy prices rose and fell through the year.

Here is the step. Now imagine that wages are settled in January after the inflation data have been released in the first, undivided example, and they pick up some fraction of last year’s annual inflation, which in turn feeds back into inflation over the following year.[3]

That step alone makes no difference. Inflation when we next measure it will still be a draw from the same distribution.

Now let’s move to twelve, monthly measurements of inflation. What happens next?

It is likely that we would also move some way towards twelve wage settlements through the year too. So, after the oil shock in February, perhaps wages respond in March. And perhaps that feeds back into the price level in April, and that feeds back into the wage settlement in May, and on into prices in June, and so on: perhaps the oil shock unlocks a wage-price spiral. The dt for wages changes in response to a change in the dt for prices.

Now, where does general price inflation end up in January the following year? Suppose oil prices fall back in September as before. Can we be sure that inflation and wage growth will, by January, have settled back to their counterfactual position too?

It’s very hard to be sure about that: it depends on the structure of, and specifically the lags in the feedback loop between prices and wages. Most likely, both wage growth and price inflation will be higher in January of the following year than they otherwise would otherwise have been. The chart below illustrates this point with arbitrary choices of positive feedback coefficients.

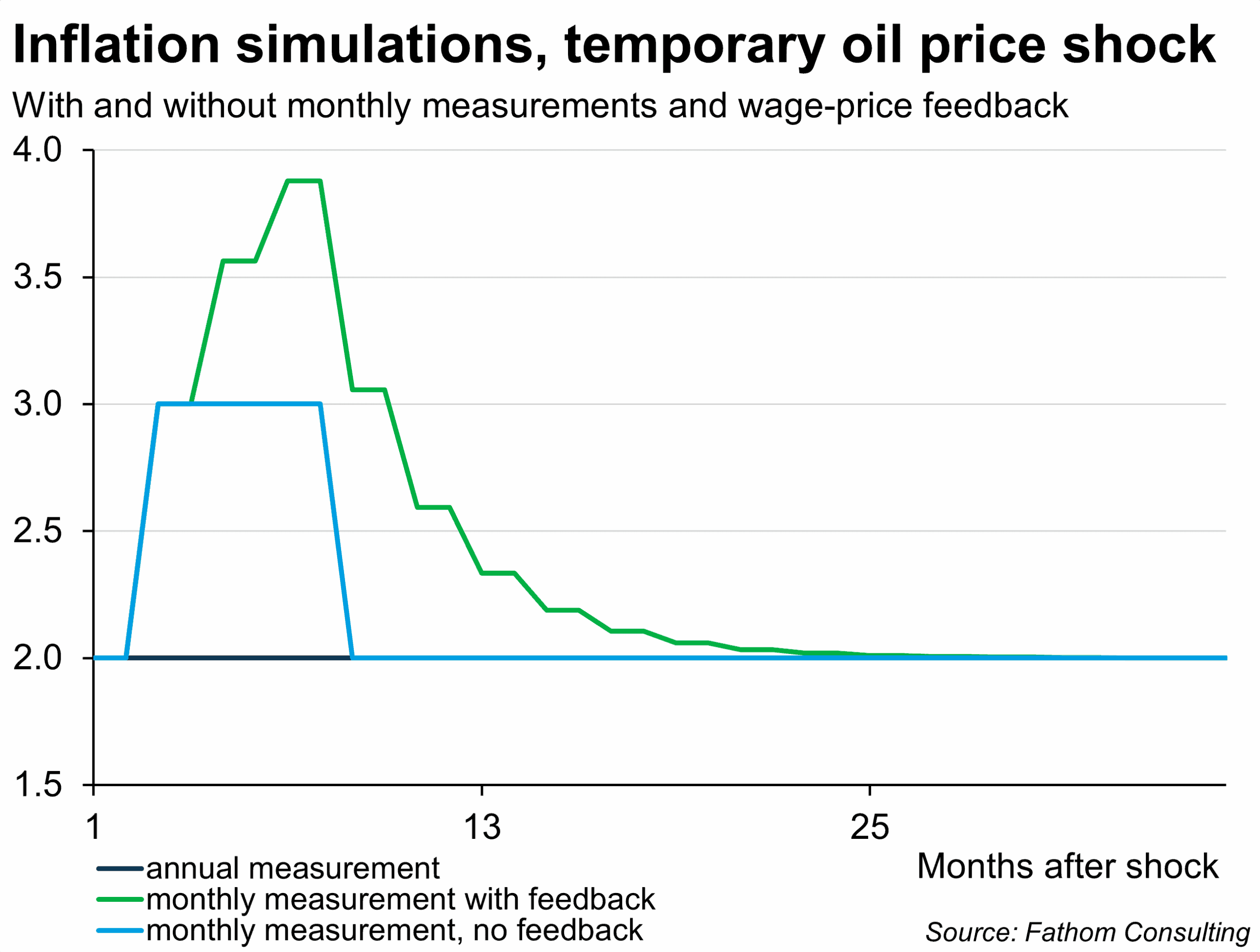
Simply by subdividing the year into twelve dts, we have changed the trajectory for prices and wages, with quite a high likelihood. It’s almost like it’s a different roll of the dice for every dt. That is because wages and prices interfere with each other, probabilistically, with a lag (they retain a ‘memory’ of previous shocks). The interference pattern depends, in part, on the frequency with which they are measured: on the dts.

In the famous two-slit experiment in quantum mechanics, photons of light can be shown to interfere with each other as long as we do not observe which slit they pass through on their way to the screen. But the interference pattern stops – or changes – once we make that observation. I don’t know whether the truth is that light is somehow ‘conscious’ of our observation or whether the observation itself has the effect of dividing an ‘indivisible stochastic process’ into two: slamming one’s hand down on the dice in mid-air, so to speak, and then rolling again (Jacob Barandes makes this argument convincingly here: https://www.youtube.com/watch?v=19Zbwle3uic ) – or whether some other process is involved. If you think you understand quantum mechanics, as Feynman supposedly said, you don’t understand quantum mechanics.

However, I can see how probabilistic variables in the real world might be sensitive to when and how frequently you measure them: how you slice up time matters for what might subsequently happen. There is no pure, weightless observer: no ‘view from nowhere’. You are an active participant, affecting the outcomes, no matter how light your touch.

There are many real-world examples of this process in action. For one, the proliferation of rolling, 24-hour ‘news’ channels (a shift from discrete to continuous time) changes how ‘news’ is perceived and that, very likely, changes what happens in the world, too. We become inured to sensational events, perhaps making those events more likely to happen.

For another, think about how you scroll through Instagram or other social media apps. Perhaps your eye snags on something – in my case, some bloke pouring cement. That snag, the momentary pause, ensures that my feed will forever after be full of people pouring cement. Each time a new cement video appears, I feel a moment’s irritation and look at the feed while swearing inwardly. That behaviour cements the algorithm, so to speak: the frequency of cement-related videos increases again.

Every time I observe the present moment, even if by accident, I change the future – specifically, the probability distribution of possible future trajectories for the thing I am observing. Whenever I stop the flow of time to look at something, I am in effect resetting future probabilities starting now, rolling the dice again.

Tony was not particularly fond of tinned food as a young man (those peas notwithstanding), but he has gradually, over time, accepted that it is his lot in life to eat a good deal of it. In the process, he has acquired a taste for the stuff, or at least learned to tolerate it.  It’s not just the flow of things that happen to you that change as a result of observation: you change yourself, too. The initially untrue assertion that Tony likes tins gradually became true.

Six days after this blog was published Tony died in France at the age of 94.
Anthony Morgan 27 March 1931 – 10 July 2025

 

[1]      The syllogism “All swans are white. This is a swan. Therefore, this is white” holds as a piece of deductive logic – if you grant the premises then the conclusion follows (of course, the first premise is not empirically true, as is now well known). But it’s curious how deductive logic like that is honoured more in the breach than in the observance in ordinary language. I remember learning at school about how double negatives, though logically implying a positive, are nearly always in fact used as emphatic negatives, for example in the Pink Floyd lyrics: “We don’t need no education”. The incorrect syllogism “All swans are white. This is white. Therefore this is a swan” is by far the more common usage in ordinary language – sometimes for comedic effect, but not always.

[2]     This is the basic (discrete-time) ‘Markovian’ process that says the future change in any variable(s) depends on its/their current momentum, the current disposition of a range of exogenous explanatory variables, and a random disturbance term that is usually assumed to be normally distributed with mean zero and a variance that reflects the past variance of the variable concerned

[3]     Or, equivalently, that inflation outturns have ‘memory’ in the sense that current shocks depend in part on historic shocks, so to know the probability distribution for future inflation it’s not enough to know current inflation: I also need to know the pattern of historic shocks to the inflationary process

 

More by this author
Why I don’t live on easy street
Intelligence is a property of systems
Reflections from a very small island