A sideways look at economics

The first time I attended a baseball match was in 2006 in Philadelphia. I was living there at the time and wanted to absorb some of the culture. Since I was ignorant of the rules, not to mention the (apparently infinite) subtleties of the game, I got chatting to the bloke sat next to me – a US citizen who’d lived in Philly for the last 20 years. He noticed my accent immediately, and the following conversation ensued.

• You’re British?
• Yes – have you ever been over there?
• Yes, often. My business is flowers: I grow flowers all over the place and ship them to wherever the market is. I grow a lot of them in the UK.
• Oh, interesting: whereabouts?
• A place called Suffolk – do you know it?
• Yes, I do! I grew up in a town called Colchester, which is in Essex but close to Suffolk.
• Oh, I know Colchester. But my operations are near a village called Stoke-by-Nayland in Suffolk.
• No way! I know Stoke really well, used to go on holiday there when I was a kid. You must know the Angel pub, then?
• Know it? That’s where I stay most times when I’m there!
• So do you know Silvana? She’s one of the barmaids there?
• Yes! I know Vana well!
• She’s my cousin.

We all have stories like that one, as the concept of six degrees of separation and the game Six degrees of Kevin Bacon illustrate. I was separated from Ken, the guy I sat next to at the baseball, by only two degrees, having a mutual friend in my cousin Silvana. Everyone has a network which grows exponentially with each degree of separation and quickly becomes entangled with the networks of everyone else.

That said, I’ve also met people in the US who, noticing my accent, say things like:

• Are you from London? London, England?
• Yes, well, kind of.
• Oh! You must know Tim!

It doesn’t always work. It is highly likely that I am connected, through a couple or three degrees, even with that person, and probably with Tim too. But those connections don’t just jump out at you. They do exist, but each link has to be painstakingly uncovered.

The exponential properties of networks have strange effects – not just connections with random strangers at baseball matches. In the UK, for example, virtually everyone is descended from William the Conqueror and also from Genghis Khan. Being able to trace your lineage from either of them does not make you special, except in the colossal waste of time and energy that uncovering the connections would represent (though being unable to find a link would indeed make you special).

The same strange exponentiality applies to networks of other entities too. Go to six degrees or more, and every corporate, financial or government entity in the world is connected to every other, just as every individual is connected to every other. Those connections flow through supply chains, through ownership structures, through trade and finance, through individuals moving between entities, and through many other vectors too.

What would happen if you tried to cut one enormous hub out of that set of overlapping global networks? The attempt would have to be a matter of degree, not of principle. In the end, we’re all related to Genghis Khan, like it or not. It’s not a question of whether you are connected, it’s a question of how strongly.

On 17 March, Fathom hosted a round-table in Washington DC whose purpose was to shed light on these questions. Given the fact that the invitees were all known to Fathom before they walked into the room, each was separated from every other by a maximum of two degrees. Beyond that, however, the complex web of connections between them was hidden.

Preparatory to that session we designed a survey, asking each participant twenty questions about how important they thought certain factors were in securing a technological advantage for the US over China. The session was held under Chatham House rules, so we cannot share the results of that survey here. But we tried the survey out on Fathom staff beforehand, and we can share those results, so here goes.

First, all the factors were judged to be important, with the average scores out of ten varying between 5.5 and 9. But, second, the ‘reveal’ in the session was the network map that we drew illustrating the hidden patterns of connectivity between the participants in the survey, in so far as they are reflected in common patterns across the answers to the survey. Common behavioural patterns, such as responses to a survey, point to underlying connectedness of which even the participants might not be aware.

In the case of Fathom, that map (or ‘minimum spanning tree’) looked like the diagram on the left below.

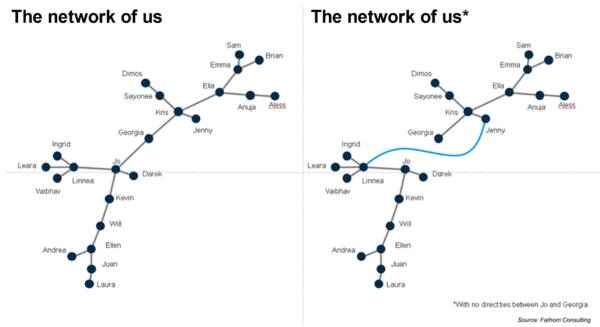
The map on the left shows the line of least resistance through all the Fathom staff who responded to the survey: the highest degree of correlation that connects every person in the system without creating a circle. The way to read it is as follows: those individuals close to the centre with many ‘branches’ springing from them (like Jo, Kris, Ella and Ellen) are ‘bellwether’ respondents. If you want a good picture of the overall mood of the meeting, talk to them. Those out on a limb far from the centre and with only one path connecting them to rest are contrarians. If you want an independent view, talk to Laura, Aless or Dimos.

The map on the left does not pick up all the connections between the individuals: in fact, everyone is connected to everyone else to a greater or lesser degree. It just picks up the highest degree of connectivity, as revealed by the correlation between survey answers.

The technique also allows us to explore ‘what-ifs’. Imagine a world in which the connections between Jo and Georgia (the pair that connect the two principal centres of gravity in the system) were severed for some reason: what would happen then? That is the map on the right. A new connection is revealed: the next most correlated pair of individuals that does not create a circle. It turns out in Fathom that pair is Linnea and Jenny. The link between Jo and Georgia may have been severed but the ecosystem grows a new link in place of that severed one, albeit a less strong link than the one that previously existed between Jo and Georgia.

That is what ecosystems do: when you damage one part of them, if the system as a whole survives, it will tend to regrow around the scar you have inflicted. It evolves around it. That is the point of a system. It has greater resilience than any individual entity would.

Weak ties, the ones that don’t make the cut to be pictured in the maps above, are ties nevertheless. The reason we feel happier when we are weakly connected to many individuals (and we do feel happier, as this Hidden Brain podcast on the topic explains) is because of the sense of security those weak ties give us. The security is the comforting feeling that there is an ecosystem supporting us. If some of my strong ties were severed, I would fall back on my weak ties and they would support me. My web of weak ties is my safety net: it gives me resilience.

What applies to individuals also applies to economic ecosystems. Some of the strong ties in the global economic ecosystem are about to be cut. We should be thinking about what are the weaker ties that will take their place, presuming the system as a whole survives. At Fathom, that’s exactly what we are thinking about. Watch this space.

 

More by this author

Only in DC

Spend, spend, spend

You gotta laff about cutting taxes